문제
삼각수 Tn(n ≥ 1)는 [그림]에서와 같이 기하학적으로 일정한 모양의 규칙을 갖는 점들의 모음으로 표현될 수 있다.
자연수 n에 대해 n ≥ 1의 삼각수 Tn는 명백한 공식이 있다.
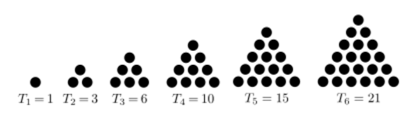
Tn = 1 + 2 + 3 + ... + n = n(n+1)/2
1796년, 가우스는 모든 자연수가 최대 3개의 삼각수의 합으로 표현될 수 있다고 증명하였다.
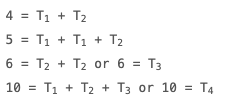
예를 들어,
이 결과는 증명을 기념하기 위해 그의 다이어리에 “Eureka! num = Δ + Δ + Δ” 라고 적은것에서 유레카 이론으로 알려졌다. 꿍은 몇몇 자연수가 정확히 3개의 삼각수의 합으로 표현될 수 있는지 궁금해졌다. 위의 예시에서, 5와 10은 정확히 3개의 삼각수의 합으로 표현될 수 있지만 4와 6은 그렇지 않다.
자연수가 주어졌을 때, 그 정수가 정확히 3개의 삼각수의 합으로 표현될 수 있는지 없는지를 판단해주는 프로그램을 만들어라. 단, 3개의 삼각수가 모두 달라야 할 필요는 없다.
입력
프로그램은 표준입력을 사용한다. 테스트케이스의 개수는 입력의 첫 번째 줄에 주어진다. 각 테스트케이스는 한 줄에 자연수 K (3 ≤ K ≤ 1,000)가 하나씩 포함되어있는 T개의 라인으로 구성되어있다.
출력
프로그램은 표준출력을 사용한다. 각 테스트케이스에대해 정확히 한 라인을 출력한다. 만약 K가 정확히 3개의 삼각수의 합으로 표현될수 있다면 1을, 그렇지 않다면 0을 출력한다.
제한
- 시간 제한 : 1초
- 메모리 제한 : 256MB
문제 풀이 과정
삼각수는 다음과 같이 나타낼 수 있다.
- T1 = 1 = 1
- T2 = 3 = 1 + 2
- T3 = 6 = 1 + 2 + 3
- T4 = 10 = 1 + 2 + 3 + 4
- T5 = 15 = 1 + 2 + 3 + 4 + 5
- T6 = 21 = 1 + 2 + 3 + 4 + 5 + 6
- T7 = 28 = 1 + 2 + 3 + 4 + 5 + 6 + 7
K의 범위는 1000 이하이다. 삼각수의 값이 1000이 넘어가는 경우는 T45이므로, T44까지의 삼각수를 미리 구해놓는다.
삼각수 3개를 합쳐서 K랑 같으면되므로, 3중 for문을 사용한다. O(45 * 45 * 45) == O(1 * T) 시간복잡도가 나온다.
정답 코드
import java.io.BufferedReader;
import java.io.InputStreamReader;
class Main10448 {
public static void main(String[] args) throws Exception {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
StringBuilder sb = new StringBuilder();
int[] triangularNumber = new int[45];
triangularNumber[1] = 1;
for (int i = 2; i < 45; i++) {
triangularNumber[i] = triangularNumber[i - 1] + i;
}
int T = Integer.parseInt(br.readLine());
while (T-- > 0) {
int K = Integer.parseInt(br.readLine());
boolean flag = false;
for (int i = 1; i < 45; i++) {
if (flag) {
break;
}
for (int j = 1; j < 45; j++) {
if (flag) {
break;
}
for (int k = 1; k < 45; k++) {
if (triangularNumber[i] + triangularNumber[j] + triangularNumber[k] == K) {
flag = true;
break;
}
}
}
}
if (flag) {
sb.append(1);
} else {
sb.append(0);
}
sb.append('\\n');
}
System.out.println(sb);
}
}
문제
삼각수 Tn(n ≥ 1)는 [그림]에서와 같이 기하학적으로 일정한 모양의 규칙을 갖는 점들의 모음으로 표현될 수 있다.
자연수 n에 대해 n ≥ 1의 삼각수 Tn는 명백한 공식이 있다.
Tn = 1 + 2 + 3 + ... + n = n(n+1)/2
1796년, 가우스는 모든 자연수가 최대 3개의 삼각수의 합으로 표현될 수 있다고 증명하였다. 예를 들어,
이 결과는 증명을 기념하기 위해 그의 다이어리에 “Eureka! num = Δ + Δ + Δ” 라고 적은것에서 유레카 이론으로 알려졌다. 꿍은 몇몇 자연수가 정확히 3개의 삼각수의 합으로 표현될 수 있는지 궁금해졌다. 위의 예시에서, 5와 10은 정확히 3개의 삼각수의 합으로 표현될 수 있지만 4와 6은 그렇지 않다.
자연수가 주어졌을 때, 그 정수가 정확히 3개의 삼각수의 합으로 표현될 수 있는지 없는지를 판단해주는 프로그램을 만들어라. 단, 3개의 삼각수가 모두 달라야 할 필요는 없다.
입력
프로그램은 표준입력을 사용한다. 테스트케이스의 개수는 입력의 첫 번째 줄에 주어진다. 각 테스트케이스는 한 줄에 자연수 K (3 ≤ K ≤ 1,000)가 하나씩 포함되어있는 T개의 라인으로 구성되어있다.
출력
프로그램은 표준출력을 사용한다. 각 테스트케이스에대해 정확히 한 라인을 출력한다. 만약 K가 정확히 3개의 삼각수의 합으로 표현될수 있다면 1을, 그렇지 않다면 0을 출력한다.
제한
- 시간 제한 : 1초
- 메모리 제한 : 256MB
문제 풀이 과정
삼각수는 다음과 같이 나타낼 수 있다.
- T1 = 1 = 1
- T2 = 3 = 1 + 2
- T3 = 6 = 1 + 2 + 3
- T4 = 10 = 1 + 2 + 3 + 4
- T5 = 15 = 1 + 2 + 3 + 4 + 5
- T6 = 21 = 1 + 2 + 3 + 4 + 5 + 6
- T7 = 28 = 1 + 2 + 3 + 4 + 5 + 6 + 7
K의 범위는 1000 이하이다. 삼각수의 값이 1000이 넘어가는 경우는 T45이므로, T44까지의 삼각수를 미리 구해놓는다.
삼각수 3개를 합쳐서 K랑 같으면되므로, 3중 for문을 사용한다. O(45 * 45 * 45) == O(1 * T) 시간복잡도가 나온다.
정답 코드
import java.io.BufferedReader;
import java.io.InputStreamReader;
class Main10448 {
public static void main(String[] args) throws Exception {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
StringBuilder sb = new StringBuilder();
int[] triangularNumber = new int[45];
triangularNumber[1] = 1;
for (int i = 2; i < 45; i++) {
triangularNumber[i] = triangularNumber[i - 1] + i;
}
int T = Integer.parseInt(br.readLine());
while (T-- > 0) {
int K = Integer.parseInt(br.readLine());
boolean flag = false;
for (int i = 1; i < 45; i++) {
if (flag) {
break;
}
for (int j = 1; j < 45; j++) {
if (flag) {
break;
}
for (int k = 1; k < 45; k++) {
if (triangularNumber[i] + triangularNumber[j] + triangularNumber[k] == K) {
flag = true;
break;
}
}
}
}
if (flag) {
sb.append(1);
} else {
sb.append(0);
}
sb.append('\\n');
}
System.out.println(sb);
}
}